乘法逆元的学习总结

以下内容均为牌王(可点开链接哦)所教，此人无敌！！！感谢牌王的细心教导，嘿嘿嘿

逆元的定义

逆元可以说是倒数概念的推广，对于正整数a,p，若有ax≡1（mod p），则称x是a关于模p的逆元。例如：

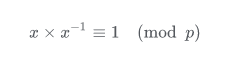
那么为什么要有逆元呢？逆元有什么作用？ 加减乘与模运算的顺序交换不会影响结果，即可用分配律，但是除法呢？答案是不行的，那么有什么办法可以完成除法与模运算之间的运算呢，这时候就是主角逆元登场了。 例如求解$(a / b) mod p$ 先求出b关于p的逆元x，即$b*x≡1 \; (mod\; p)$，将其带入上式得 $(\frac{a}{b} * b * x)≡ 1 (mod p) -> (a * x)≡1(mod\; p)$ 即可将除法转化成乘法，是不是很有趣？ 逆元存在的条件：a与p互质，即gcd(a,p)=1。

求解逆元的三种方法

  1. ==费马小定理== 当p为素数时，则有

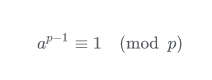
将其变形为

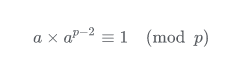
由逆元定义可知，$a^{p-2}$就是逆元

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
ll FPM(ll x,ll power,ll mod)
{
    ll ans = 1;
    while(power)
    {
        if(power & 1)
        {
            ans = (ans * x) % mod;
        }
        x = (x * x) % mod;
        power >>= 1;
    }
    return ans % mod;
}
  1. ==扩展欧几里得算法==

ax≡1(mod p)->ax = pk + 1 当a，p互质时，gcd(a,b)=1，即将上式转化为

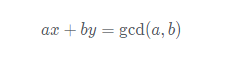
当求解gcd(a,b)时，递归结束的条件为b=0，得出a=gcd(a,b)，进一步得出x=1,所以对上式使用递归时，结束条件为b = 0，并使x=1，y=0。 即

1
2
3
4
5
6
if(!b)
{
    x = 1;
    y = 0;
    return a;
}

紧接着一直回朔，最后得出x的值，并且还可以求出a和b的最大公约数，是不是一举两得？

回朔过程的解析： $a*x1+b*y1=gcd(a,b)$ $a*x2+b*y2=gcd(a,b)$ 将第二个式子变化一下为 $bx2+(a-a/b*b)*y2=gcd(a,b)->ay2+b(x2-a/b*y2)=gcd(a,b)$ 则$x1=y2, y1=x2-a/b*y2$ 那么不断回朔回去，即可得到x。

得出$x$后，如果为负数，则需要$(x\% mod + mod) \% mod$使其变为正

当然，可以将其推广则可求出任意二元一次方程的最小解，不过也是有条件的，例如 求ax+by=c的解，当且仅当$c是gcd(a，b)$的倍数时，$x$有最小解。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
typedef long long ll;
ll exgcd(ll a,ll b,ll &x,ll &y) //扩展欧几里得算法
{
    if(b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    ll ret = exgcd(b, a % b, x, y);
    ll t = x;
    x = y;
    y = t - a / b * x;
    return ret;
}
ll inv(int a, int mod)  //求a在mod下的逆元，如果不存在返回-1
{
    ll x, y;
    ll d = exgcd(a, mod, x, y);
    return d ? (x % mod + mod) % mod : -1;
}

  1. ==线性递推==

    过程如下： 在这里插入图片描述 这里就不再详细描述了……直接上代码！！！(打字太累了)

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
ll inv[3000005] = {0 , 1}; //n等于1时，关于mod的逆元就为1
int main()
{
    ll n, mod;
    scanf("%lld%lld",&n,&mod);
    printf("1\n");
    for(int i = 2;i <= n; i++) // 从二开始，防止改变inv[1]的值
    {
        inv[i] = mod - (mod / i) * inv[mod % i] % mod;// 这一步important // 加个mod是为了防止逆元为负
        printf("%lld\n",inv[i]);
    }
    return 0;
}

狙击美佐第一篇博客的感想

很早就想自己写点东西记录自己的学习过程，可以太懒了，而且语言组织也不好，不过，在数论方面，每次我遇到问题，牌王都会帮我解答，非常感谢牌王！！！那么这次我就将这篇博客写好，“送”给你来表达我对你的爱？

本文作者：jujimeizuo
本文地址： https://blog.jujimeizuo.cn/2020/05/15/mulinv/
本博客所有文章除特别声明外，均采用 CC BY-SA 3.0 协议。转载请注明出处！