今天高数老师上了无穷级数的p级数,不过没有讲到著名的巴塞尔问题,所以我来描述一下。
巴塞尔问题是在1644年被提出,后来在1735年被欧拉大神给解决了。
问题描述
计算所有平方数的倒数之和,也就是2-级数:
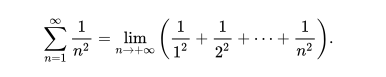
我们知道调和级数是发散的,但是这个级数是不是发散的呢?答案是收敛的,大小大概是1.644934,是不是和提出问题的时间有点相似?
欧拉大神的想法
那个时候欧拉的手里有两个正弦函数:

这其实就是泰勒展开!
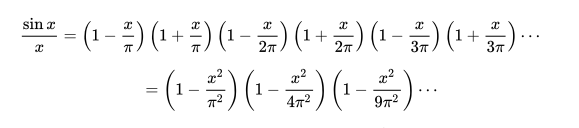
将第一个等式左右同除x得第三个等式:

那第二个等式是怎么来的呢? 我们知道sinx / x = 0的根出现在x = nπ,n = ±1、±2、±3…所以sinx / x可以像因式分解一样转化成上图。
如果我们把第二个等式右边所有的x^2^的系数加起来得:
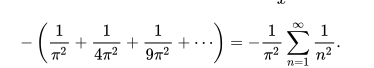
在和第三个等式中x^2^的系数相等得:
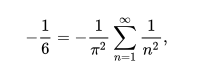
等式两边乘-π^2^,得:
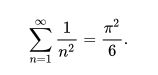
所以欧拉大神解决了著名的巴塞尔问题在当时是十分轰动的,不得不佩服这些伟人的智慧。
这很好地将无穷级数和π结合起来,其实π是非常神奇的数字,包括自然底数e也是,这些数字的由来都非常有趣,只要是数学上的都有趣!!!
本文作者:jujimeizuo
本文地址: https://blog.jujimeizuo.cn/2020/05/21/basel-problem/
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0 协议。转载请注明出处!