P4157 [SCOI2006]整数划分

传送门：https://www.luogu.com.cn/problem/P4157

借鉴大佬：https://blog.csdn.net/oampamp1/article/details/108919448

题意

给一个整数N，将他拆成若干整数，求他们乘积最大值。

思路

$先将题目转化一下：$

$$已知\sum_{i=1}^n x_i=N，求max{\prod_{i=1}^n x_i}\;\;\;\;(n表示x_i有几项)$$

$首先根据均值不等式（调和\leq 几何\leq 算术 \leq 平方）：$ $$\frac{n}{\sum_{i=1}^n\frac{1}{x_i}}\leq \sqrt[n]{\prod_{i=1}^nx_i}\leq \frac{\sum_{i=1}^nx_i}{n}\leq \sqrt[n]\frac{\sum_{i=1}^nx_i^2}{n}$$

$所以可以得到：$ $$\frac{\sum_{i=1}^nx_i}{n}\ge \sqrt[n]{\prod_{i=1}^nx_i}$$

$$\left( \frac{\sum_{i=1}^nx_i}{n} \right)^n\ge \prod_{i=1}^nx_i$$

$观察上式，要使乘积最大，那需要尽量取等号，所以x_i要尽量平均，所以得到下式：$

$$\left( \frac{N}{n} \right)^n= \prod_{i=1}^nx_i$$

$令y=(\frac{N}{n})^n，两边同时取对数得：$

$$\ln y=n\ln N-n\ln n$$

$两边同时对n求导得：$

$$\frac{y’}{y}=\ln N-ln n - 1$$

$$得y’=(\ln N-\ln n - 1)(\frac{N}{n})^n$$

$令y’=0，因为(\frac{N}{n})^n>0，所以\ln N-\ln n - 1=0，即：$

$$n=e^{\ln N - 1}=\frac{N}{e}$$

$由于n是在整数域里，所以n只有两个选择\frac{N}{2}和\frac{N}{3}，那么该取哪一个呢？$

$刚开始的\prod_{i=1}^nx_i=(\frac{N}{n})^n=2^{\frac{N}{2}}或3^{\frac{N}{3}}，现在就看哪个大。$

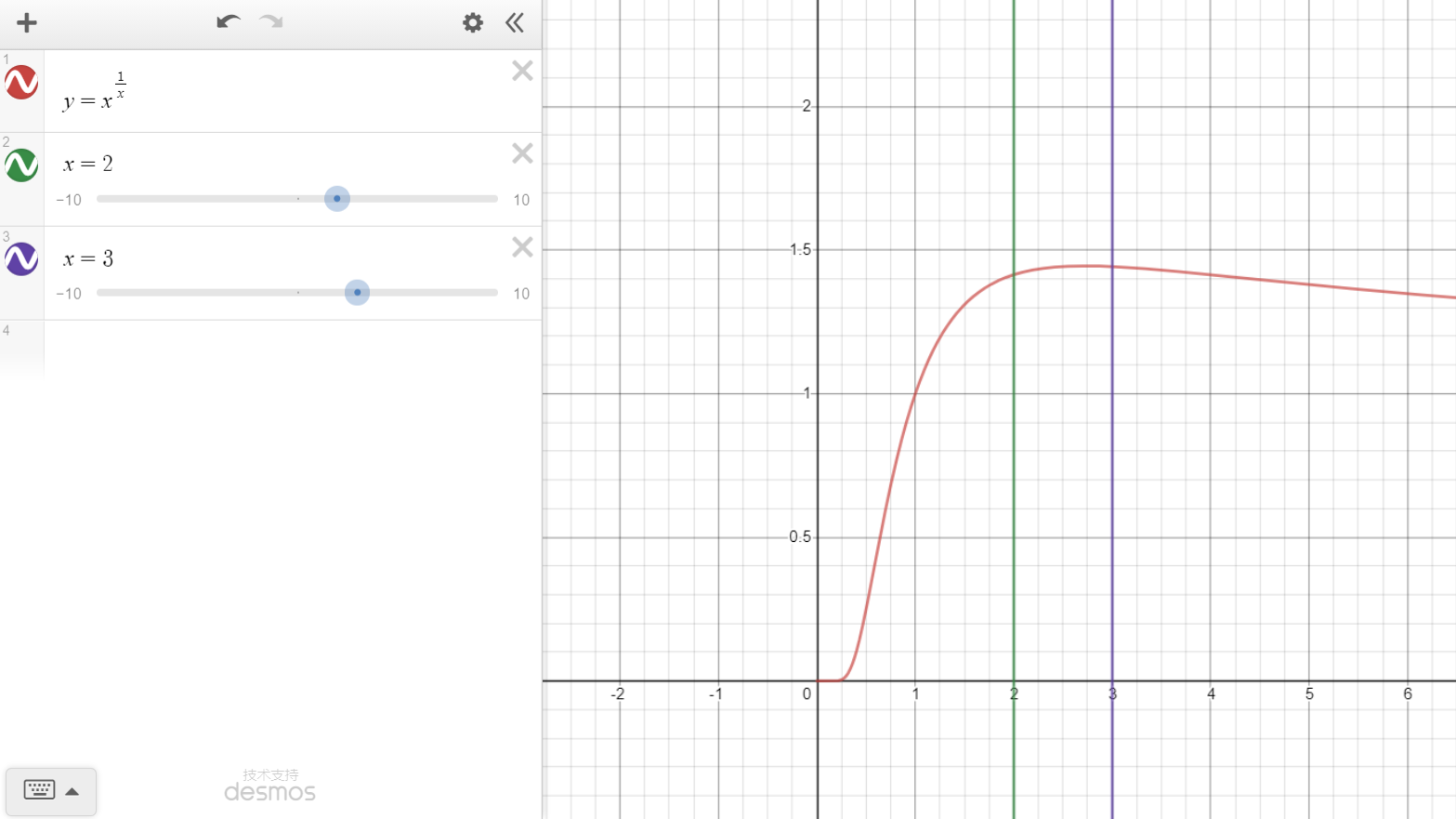
$根据上图可知，2^{\frac{N}{2}}<3^{\frac{N}{3}},当然也可以手动算一下。$

$所以得\prod_{i=1}^nx_i=3^{\frac{N}{3}}最大，即优先取3，没有3取2，总之，推导到最后就是个憨憨题。总结一下：$

$让N mod \;3:$

$- N mod\; 3=0，全部拆成3，ans=3^{\frac{N}{3}}$ $- Nmod\;3=1，拿出一个3然后加1组成4，其他都为3，ans=3^{\frac{N-1}{3}-1}*4$ $-Nmod\;3=2，拿出一2，其他都为3，ans=3^{\frac{N-2}{3}}*2$

由于答案爆longlong，所以用JAVA大数，这不比高精度香吗？

Code（67MS）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

import java.util.*;
import java.math.*;
import static java.lang.Math.min;

public class Main
{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        int N;
        N = in.nextInt();
        BigInteger ans = new BigInteger("1");
        if(N % 3 == 0) {
            ans = BigInteger.valueOf(3).pow((N / 3));
        }
        else if(N % 3 == 1) {
            ans = BigInteger.valueOf(3).pow((N / 3 - 1)).multiply(BigInteger.valueOf(4));
        }
        else if(N % 3 == 2) {
            ans = BigInteger.valueOf(3).pow((N / 3)).multiply(BigInteger.valueOf(2));
        }
        String s = ans.toString();
        System.out.println(s.length());
        for(int i = 0;i < min(100, s.length()); i++) {
            System.out.print(s.charAt(i));
        }
        System.out.println();
    }
}

本文作者：jujimeizuo
本文地址： https://blog.jujimeizuo.cn/2020/10/08/luogu-p4157/
本博客所有文章除特别声明外，均采用 CC BY-SA 3.0 协议。转载请注明出处！