2020ICPC上海站 I题 Sky Garden 数学推导+思维

传送门：https://ac.nowcoder.com/acm/contest/9925/I 参考：https://blog.csdn.net/qq_43750980/article/details/111297783

题意

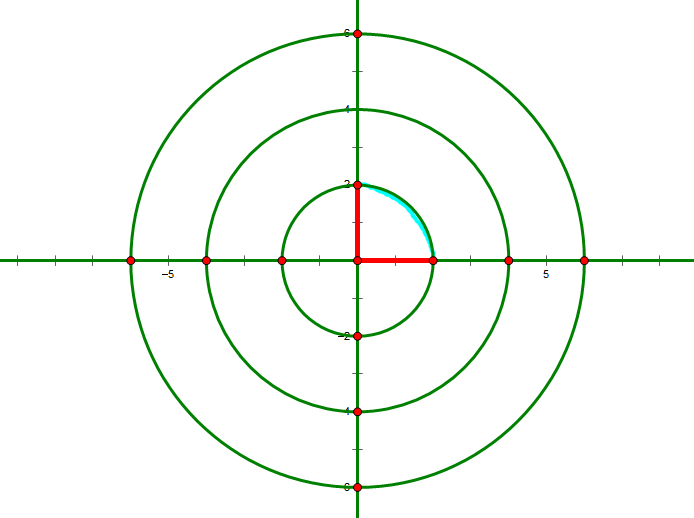
有n个同心圆，圆心都为（0，0），半径依次递增1,2…n 有m条直线将这n个圆等分成2*m份，直线和圆会有交点。 一个交点走向另一个交点只能走有线的路径。

求所有点对距离和。

$$\sum_{i,j\in R\;i\ne j}dis(i,j)$$

题意

这题关键是一个点怎么走向另一个点，这很重要！ 首先猜测两个结论：

  • 结论一：在同一圆上的两点，最短距离为min(两点最短弧长，圆的直径)。

  • 结论二：不同圆上的两点，外圆需要沿直径走向内圆的大一圈的外圆，再按照结论一走。

所以我们可以从小圆推到大圆，接下来就开始操作。

  1. 首先预处理半径为1时，一个点到其他所有点的距离和。

  2. 维护两个数组，a[i]和b[i] a[i]表示[1,i]个圆内，从1个点出发到该圆内其他所有点的距离和

    b[i]表示在第i个圆上，从1个点出发到该圆上其他所有点的距离和

  3. 从i=2开始递推，从第i-1个圆推向第i个圆时 b[i]只是从半径为1增大了i倍，所以b[i] = b[1] * i（结论一） a[i]首先要先加b[i]和a[i -1]，所以第i和i-1层以内都处理好了。 接着就是第i层的点到所有内层点的距离怎么算? 只需要将第i个圆内层所有点（包括第i个圆上所有点）往里进一层即可（结论二）

    1. O(n)处理每一层圆得答案

具体看代码

Code（3MS）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

##include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef long double ld;
typedef pair<int, int> pdd;

##define INF 0x3f3f3f3f
##define lowbit(x) x & (-x)
##define mem(a, b) memset(a , b , sizeof(a))
##define FOR(i, x, n) for(int i = x;i <= n; i++)

// const ll mod = 998244353;
// const ll mod = 1e9 + 7;
// const double eps = 1e-6;
 const double PI = acos(-1);
// const double R = 0.57721566490153286060651209;

const int N = 1e5 + 10;
double a[N], b[N];

void solve() {
    int n, m; scanf("%d%d",&n,&m);

    /*  一个点到其他所有点的总距离和（半径为1）   */
    double cnt = 0;
    for(int i = 1;i < m; i++) {
        if(PI * i < 2.0 * m) cnt += PI * i / m;
        else cnt += 2.0;
    }
    cnt *= 2.0; cnt += 2.0;
    a[1] = b[1] = cnt;

    // a[i]表示[1,i]个圆内，从1个点出发到该圆内其他所有点的距离和
    // b[i]表示在第i个圆上，从1个点出发到该圆上其他所有点的距离和

    /*  O(n)递推，从第1个圆推到第n个圆  */
    for(int i = 2;i <= n; i++) {
        // 半径扩大i倍（结论一支撑）
        b[i] = b[1] * i;
        // 内层的每一个点都要往里走一层，每一层的一个点需要走2*m次，然后的2*m的走法根据之前推的走法走（结论二支撑）
        a[i] = a[i - 1] + b[i] + 2.0 * m * (i - 1);
    }

    /*  O(n)求解答案  */
    double ans = 0;
    for(int i = 1;i <= n; i++) {
        ans += 2.0 * m * (a[i] - b[i]) + 2.0 * m / 2.0 * b[i];
        // m * b[i] 表示，第i个圆上，任意两点之间的距离和，因为2*m点，但是会重复计算1倍，所以要除2
        // 2 * m * (a[i] - b[i]) 表示，第i个圆上任意一点到该圆内其他所有点的距离和，因为有2*m个点（去掉第i个圆上的点距离和）
        if(m > 1) ans += 2.0 * i * m; // m>1即原点也算一点，特殊处理
    }
    printf("%.10lf\n",ans);
}

signed main() {
    sovle();
}

本文作者：jujimeizuo
本文地址： https://blog.jujimeizuo.cn/2020/12/17/2020-icpc-shanghai-i/
本博客所有文章除特别声明外，均采用 CC BY-SA 3.0 协议。转载请注明出处！