【2021牛客寒假第一场】H题 幂塔个位数的计算 欧拉降幂

传送门：https://ac.nowcoder.com/acm/contest/9981/H 今天被大一按在地上摩擦，很不爽（估计以后都是，呜呜呜

题意

求$a \uparrow \uparrow n$的最后一位。

小知识：$\uparrow$ 这个符号是高德纳箭头，感兴趣的小伙伴可以自行百度，和已知的最大数有关联。

思路

在我学欧拉降幂的时候，做过这样的一个题目，求$2^{2^{2^{…}}} mod\;p$。 注意：是无穷多个，而不是有限个。

所以这很好地告诉我们，当幂次巨大时，mod之后基本上不会发生什么变化了。这一题只不过是\%10而已。

$要解决这一题，我们需要知道一个知识点：欧拉降幂

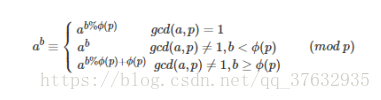
因为我们的p是10，不一定满足朴素版欧拉降幂。所以需要下面的广义欧拉降幂。

当我们要求$a^{a^{a^{a…}}} \%10$时，用广义欧拉降幂可得：

$$a^{a^{a^{a^{a^{…} \%1} \%2 + 2}} \%4 + 4} \%10$$

我们会发现，当n>3时，整个式子变成了$a^{a \%4+4}\%10$ 所以我们有三种讨论方式：

  • n=1时，直接输出最后一位
  • n=2时，答案为$a^{a \%4+4} \%10$
  • n=3时，答案为$a^{a^{a \%2+2} \%4+4} \% 10$
  • n>3时，答案为$a^{a \%4+4} \%10$

所以，就完事了。

题解给的就是找规律暴力求解，但它内含的就是欧拉降幂的思想。

Code(9MS)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
##include "bits/stdc++.h"

using namespace std;

typedef long long ll;

void solve() {
    string a, n; cin >> a >> n;
    ll t = a[a.length() - 1] - '0';
    if(n == "1") {
        cout << t << endl;
    }
    else {
        ll tmp1, tmp2;
        if(n == "2") tmp1 = 1;
        else tmp1 = t % 2 + 2;
        ll mod4 = 0;
        for(int i = 0;i < a.length(); i++) {
            mod4 = mod4 * 10 + a[i] - '0';
            mod4 %= 4;
        }
        tmp2 = 1;
        for(int i = 1;i <= tmp1; i++) {
            tmp2 = tmp2 * mod4 % 4;
        }
        tmp2 += 4;
        ll ans = 1;
        for(int i = 1;i <= tmp2; i++) {
            ans = ans * t % 10;
        }
        cout << ans << endl;
    }
}

signed main() {
    solve();
}

本文作者：jujimeizuo
本文地址： https://blog.jujimeizuo.cn/2021/02/01/2021-nowcoder-hanjia-1-h/
本博客所有文章除特别声明外，均采用 CC BY-SA 3.0 协议。转载请注明出处！