机器学习 K-means算法（二维）

2021年数学建模美赛用到该算法，特记此文。

K-means算法中文名为K-均值聚类算法。

聚类

聚类（Clustering）：就是对大量未知标注的数据集，按数据的内在 相似性将数据集划分为多个族（Cluster），使族内的数据相似度 尽可能大而类别间的数据相似度尽可能小。

为什么要聚类：客户分割（segmentation）是一种发现用户特性的方法。 v 将一个基于数据的客户信息分组；从而给你一个客户信息的概况， 这可以直接转化为针对不同客户的营销策略。

应用领域：

经济领域：

  • 帮助市场分析人员从客户数据库中发现不同的客户群
  • 对住宅区进行聚类，确定自动提款机ATM的安放位置
  • 股票市场板块分析，找出最具活力的板块龙头股
  • 企业信用等级分类

生物学领域：

  • 推导植物和动物的分类
  • 对基因分类，获得对种群的认识

其他：

  • 作为其他数学算法的预处理步骤，获得数据分布状况

原理：

聚类分析中“类”的特征：

  • 聚类所说的类不是事先给定的，而是根据数据的相似性和距 离来划分；
  • 聚类的数目和结构都没有事先假定

聚类方法的目的是寻找数据中：

  • 潜在的自然分组结构
  • 感兴趣的关系

K-means算法概述

K是什么？ K是聚类算法当中类的个数。

means是什么？ means是均值算法。

Summary：K-means是采用均值算法把数据分成K个类的硬聚类算法！

对于连续型属性具有较好的聚类效果，不适合处理离散型属性。

K-means评价标准

一个好的聚类方法要能产生高质量的聚类结果—簇，这些簇要具备以 下两个特点：

  • 高的簇内相似性
  • 低的簇间相似性

基本思想：属于划分方法（partitioning method），通过迭代把数据集 划分为不同的类别（或称簇），使得评价聚类性能的准则函数达到最 优，使得每个聚类类内紧凑，类间独立。

算法基本流程

  1. 随机抽取k 个点作为初始聚类的中心，由各中心代表各聚类
  2. 计算所有点到这k个中心的距离，并将点归到离其最近的聚类
  3. 调整聚类中心，即将聚类的中心移动到聚类的几何中心（即平均值）
  4. 重复第2、3步直到聚类的中心不再移动，此时算法收敛

K-means算法主要因素

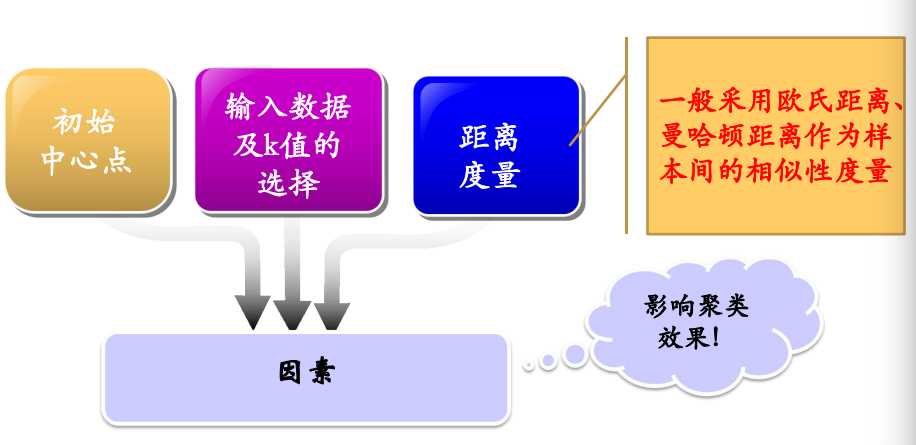
K-means优缺点

优点:

  1. 思想简单易行
  2. 时间杂度接近线性
  3. 对大数据集，具有高效性和可伸缩性

缺点：

  1. 依赖于初始均值的选择
  2. 须事先给定聚类数k值
  3. 对噪声和孤立数据敏感

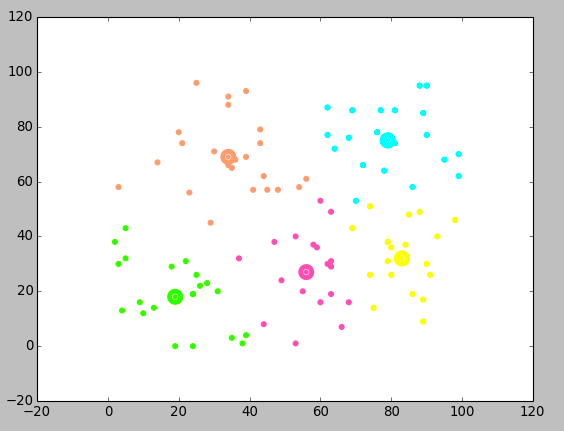
python实现二维K-means算法并用matplotlib实现画图

这里的数据是随机数据，只需要改一下输入方式即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import numpy as np
import matplotlib.pyplot as plt

def distance(e1, e2):
    return np.sqrt((e1[0] - e2[0]) ** 2 + (e1[1] - e2[1]) ** 2)

def means(arr):
    return np.array([np.mean([e[0] for e in arr]), np.mean([e[1] for e in arr])])

def farthest(k_arr, arr):
    f = [0, 0]
    max_d = 0
    for e in arr:
        d = 0
        for i in range(k_arr.__len__()):
            d = d + np.sqrt(distance(k_arr[i], e))
        if d > max_d:
            max_d = d
            f = e
    return f

def closest(a, arr):
    c = arr[1]
    min_d = distance(a, arr[1])
    arr = arr[1:]
    for e in arr:
        d = distance(a, e)
        if d < min_d:
            min_d = d
            c = e
    return c

if __name__ == "__main__":

    arr = np.random.randint(100, size=(100, 1, 2))[:, 0, :]

    m = 5
    r = np.random.randint(arr.__len__() - 1)
    k_arr = np.array([arr[r]])
    cla_arr = [[]]
    for i in range(m - 1):
        k = farthest(k_arr, arr)
        k_arr = np.concatenate([k_arr, np.array([k])])
        cla_arr.append([])

    n = 20
    cla_temp = cla_arr
    for i in range(n):
        for e in arr:
            ki = 0
            min_d = distance(e, k_arr[ki])
            for j in range(1, k_arr.__len__()):
                if distance(e, k_arr[j]) < min_d:
                    min_d = distance(e, k_arr[j])
                    ki = j
            cla_temp[ki].append(e)

        for k in range(k_arr.__len__()):
            if n - 1 == i:
                break
            k_arr[k] = means(cla_temp[k])
            cla_temp[k] = []

    col = ['HotPink', 'Aqua', 'Chartreuse', 'yellow', 'LightSalmon']
    for i in range(m):
        plt.scatter(k_arr[i][0], k_arr[i][1], linewidth=10, color=col[i])
        plt.scatter([e[0] for e in cla_temp[i]], [e[1] for e in cla_temp[i]], color=col[i])
    plt.show()

本文作者：jujimeizuo
本文地址： https://blog.jujimeizuo.cn/2021/02/15/k-means/
本博客所有文章除特别声明外，均采用 CC BY-SA 3.0 协议。转载请注明出处！