数字图像处理期末复习（三）数字图像的基本运算

3.1 灰度直方图

3.1.1 定义

灰度直方图是反映一幅图像中各灰度级像素出现的频率，反映灰度分布情况。横坐标用于表示像素的灰度级别，纵坐标用于表示该灰度出现的频数。

3.1.2 特征

  1. 只能反映灰度分布，丢失像素位置信息
  2. 一幅图像对应唯一灰度直方图，反之不一定
  3. 一幅图像分成多个区域，多个区域的直方图之和是原图像的直方图

3.13 理解规则

  1. 左黑右白，左暗右亮
  2. 横轴上各（亮度值）点对应的柱状高度就是分布在该亮度的像素个数
  3. 当柱状接近分布在整个横轴上，且至少有一个峰值时，图像的对比度较好

3.1.4 应用

  • 判断图像量化是否恰当
  • 确定图像二值化的阈值

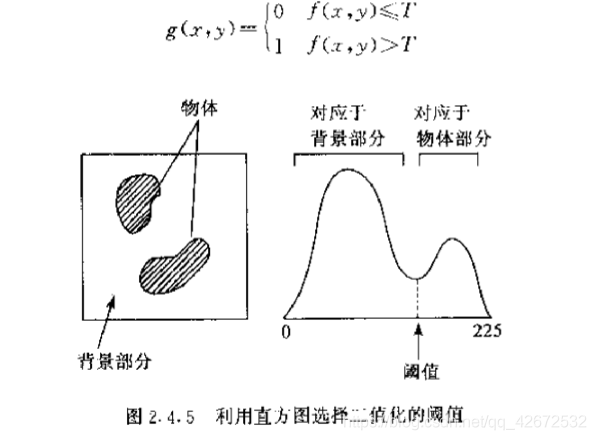
  • 物体部分灰度值比其他部分灰度值大的时候可以统计图像中物体面积
  • 计算图像信息量（熵）

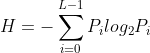
3.1.5 彩色图像转换成灰度图像

1
2
im = cv2.imread('lenna.jpg')
nim = cv2.cvtColor(im,  cv2.COLOR_BGR2GRAY);

3.1.6 计算直方图

OpenCV计算直方图的函数：calcHist()

例如：打开图像 lenna.jpg，使用 cv2.calcHist()函数计算灰度图像的直方图，以屏显打印输出的形式显示具有 100-128 灰度值的像素数目；

1
2
3
4
5
6
7
import cv2
import matplotlib.pyplot as plt
im = cv2.imread('lenna.jpg')
nim = cv2.cvtColor(im,  cv2.COLOR_BGR2GRAY)
jpg = cv2.calcHist([im], [0], None, [29], [100, 128])
plt.plot(jpg)
plt.show()

 

3.2 归一化直方图

3.3 图像的基本运算

3.3.1 点运算

点运算：是指对一幅图像中每个像素点的灰度值进行计算

点运算的效果：点运算可以改变图像数据所占据的灰度值范围，从而改善图像显示效果

点运算的分类：线性点运算，非线性点运算

线性点运算：灰度变换函数形式可以采用线性方程描述

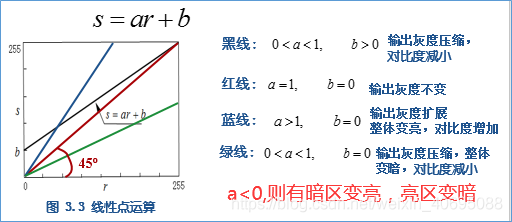
非线性点运算：非线性点运算的输出灰度级与输入灰度级呈非线性关系，常见的非线性灰度变换为对数变换和次幂变换

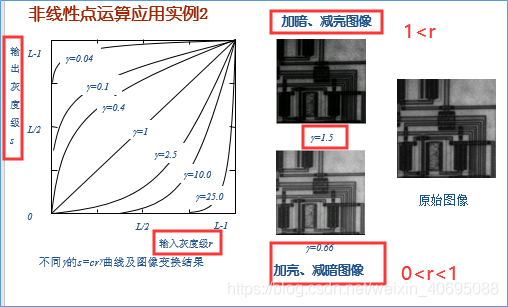
注意：

  • 点运算是否会改变图像内像素点之间的空间位置关系？

不会！点运算是一种像素的逐点运算，它与相邻的像素之间没有运算关系，点运算不会改变图像内像素点之间的空间位置关系。

  • 对图像灰度的拉伸，非线性拉伸与分段线性拉伸的区别？

非线性拉伸不是通过在不同灰度值区间选择不同的线性方程来实现对不同灰度值区间的扩展与压缩。而是在整个灰度值范围内采用统一的非线性变换函数。利用函数的数学性质实现对不同灰度值区间的扩展与压缩。

3.3.2 代数运算

代数运算：将两幅或多幅图像通过对应像素之间的加、减、乘、除运算得到输出图像。

加法运算：通常用于平均值降噪的场合。

减法运算（差影法）：检测同一场景两幅图像之间的变化；混合图像的分离；消除背景影响。

乘法运算：图像的局部显示；改变图像的灰度级

除法运算：可用于改变图像的灰度级

3.3.3 逻辑运算

逻辑运算：将两幅或多幅图像通过对应像素之间的逻辑与、或、非运算得到输出图像

“与”、“或”逻辑运算可以从一幅图像中提取子图像。

3.3.4 几何运算

几何运算：改变图像中物体对象（像素）之间的空间关系。几何变换可以分为图像的位置变换（平移、镜像、旋转）、形状变换（放大、缩小）以及图像的复合变换等。

图像的平移

图像的镜像：水平镜像和垂直镜像

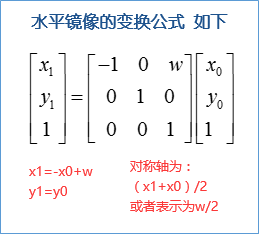
图像的旋转

以图像的中心为原点，旋转一定的角度，即将图像上的所有像素都旋转一个相同的角度。

注意：

  • 图像旋转之后，由于数字图像的坐标值必须是整数，因此，可能引起图像部分像素点的局部改变，所以，这时图像的大小也会发生一定的改变。
  • 为了避免图像信息的丢失，图像旋转之后必须进行平移变换（或者先平移，在旋转）。
  • 图像旋转之后，会出现许多空洞点，我们需要对这些空洞点必须进行填充处理，进行插值处理

图像的缩放

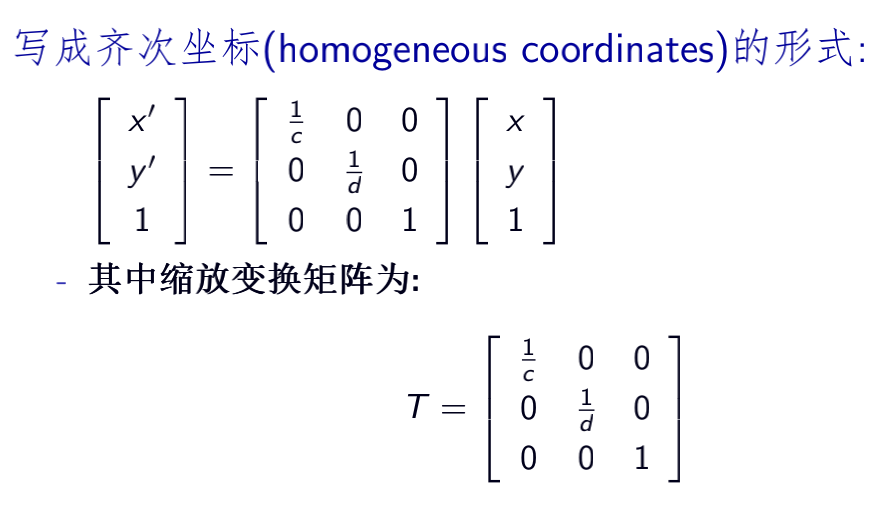
3.3.5 灰度插值

在图像放大的正变换中，出现很多空格，因此，需要对放大后所多出来的一些空格填入适当的像素值。一般采用最近邻插值和线性插值法。

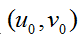
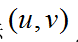
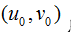
最邻近插值：最近邻法是将 点最近的整数坐标 点的灰度值取为点的灰度值。

在该点各相邻像素间灰度变化较小时，这种方法是一种简单快捷的方法，但当该点相邻像素间灰度差很大时，这种灰度估值方法会产生较大的误差。计算简单，容易产生锯齿现象。

双线性插值法：是最邻近法的改进版，效果较好，但是具有低通滤波性，使高频分量受损，图像轮廓受损。会引入平滑效应，使图像产生模糊，清晰度下降。可以采用效果更好的三次内插法。

三次内插法：可精确地恢复原函数，当然也就可精确得到采样点间任意点的值。此方法计算量很大，但精度高，能保持较好的图像边缘。

本文作者：jujimeizuo
本文地址： https://blog.jujimeizuo.cn/2021/06/16/shuzituxiang3/
本博客所有文章除特别声明外，均采用 CC BY-SA 3.0 协议。转载请注明出处！