大整数相乘 - 模拟/分治/FFT/CRT/网络流/Furer

问题描述

有两个超过long long类型的大整数X和Y，用较低的复杂度求解X*Y。

六种方法

方法一：模拟

时间复杂度：$O(n^2)$

思路

模拟乘法的过程，一个数的第i位和另一个数的第j位相乘，一定会累加到结果的第i+j位，结果的数组一个数组元素存2位数，最后对结果整除得到进位，mod得到余数就是i+j位的数字，最后打印出来。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
std::vector<int> multiply(std::string s, std::string t) {
    int n = (int) s.size(), m = (int) t.size();
    reverse(s.begin(), s.end());
    reverse(t.begin(), t.end());
    std::vector<int> ans(n + m + 1);
    for (int i = 0; i < n; i++) {
        int bit = 0;
        for (int j = 0; j < m  bit; j++) {
            int now = ans[i + j] + (s[i] - '0') * (t[i] - '0') + bit;
            ans[i + j] = now % 10;
            bit = now / 10;
        }
    }
    while (ans.back() == 0) {
        ans.pop_back();
    }
    return ans;
}

方法二：分治

时间复杂度：$O(n^{log^3}) \approx O(n^{\frac{3}{2}}) \approx O(n^{1.59})$

思路

分治算法解题的一般步骤：

分解：将要解决的问题划分为若干个规模较小的同类问题 求解：当子问题划分的足够小时，用较简单的方法解决 合并：按原问题的要求，将子问题的解逐层合并构成原问题的解

X和Y的位数相同

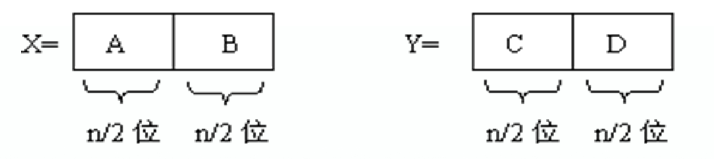
X和Y的位数相同

$$ X = A_{10}^{\frac{n}{2}}+B \quad Y=C_{10}^{\frac{2}{n}} + D $$

$$ XY = (A_{10}^{\frac{n}{2}}+B)_(C*10^{\frac{n}{2}}+D) $$

$$ XY = AC_{10}^n+(AD+BC)_{10}^{\frac{2}{n}}+BD $$

计算成本：我们必须进行4次n/2位整数的乘法(AC，AD，BC和BD)，以及3次不超过n位的整数加法此外还要做2次移位。所有这些加法和移位共用O（n）步运算。设T（n）是2个n位整数相乘所需的运算总数，我们有：

$$ T(n) = O(1) \quad n = 1 $$

$$ T(n)=4T(n/2)+O(n) \quad n > 1 $$

得：

$$T(n) = O(n^2)$$

这种方法不见得比暴力更有效，所以需要改进一点，变换上式得：

$$ XY=AC_{10}^n + ((A-B)_(D-C) + AC+BD)*10^{\frac{2}{n}}+BD $$

计算成本：3次n/2位乘法，6次不超过n位加减法，2次移位，所有加法和移位共计O(n)次运算。我们有：

$$ T(n) = O(1) \quad n = 1 $$

$$T(n)=3T(n/2) + O(n) \quad n > 1$$

得：

$$T(n) = O(n^{log^3}) \approx O(n^{\frac{3}{2}}) \approx O(n^{1.59})$$

X和Y的位数不同

和位数相同同理

假设 n1为B的位数，B属于低位的那一部分 n2为A的位数，A属于高位的那一部分 m1为D的位数，D属于低位的那一部分 m2为D的位数，C属于高位的那一部分

$$XY=(A_{10}^{n_2}+B)_(C*10^{m_2}+D)+BD$$

$$XY=AC_{10}^{n_2+m_2}+(AD_{10}^{n_2}+BC*10^{m_2})+BD$$

上式一共需要进行2次n2的乘法（AC、AD各一次）、2次m2的乘法（AC、BC各一次）和3次加法，因而该算法的时间复杂度为

$$T(m + n) = 2T(m) + 2T(n)+O(m+n)$$

跟上面一样，对AD+BC进行分解优化得：

$$XY=2_AC_{10}^{n_2+m_2}+(A_{10}^{n_2}-B)_(D-C_{10}^{m_2}) + 2_BD$$

修改后的时间复杂度为：

$$T(m+n) = T(m) + T(n) + T(min(n, m)) + O(m + n)$$

由于$T(min(n,m)) < T(m)+T(n) $，所以修改后的算法更好，时间复杂度为

$$T(n) = O(n^{log^3}) \approx O(n^{\frac{3}{2}}) \approx O(n^{1.59})$$

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
std::vector<int> solve(std::string X, std::string Y) {
    std::vector<int> result(255, 0);
    std::function<void(std::string, std::string, int)> multiply = [&](std::string s, std::string t, int pos) {
        int n = (int) s.size(), m = (int) t.size();
        if (n == 0  m == 0) {                 // 位数为0时
            return ;
        } else if (n == 1 && m == 1) {          // 递归到当前数组s和t的位数全为1时
            result[pos] += (s[0] - '0') * (t[0] - '0');
            return ;
        } else {                                // 当数组s和t的位数至少有一个不为1时
            int n1 = n / 2;                     // n1为B的位数，B属于低位的那一部分
            int n2 = n - n1;                    // n2为A的位数，A属于高位的那一部分
            int m1 = m / 2;                     // m1为D的位数，D属于低位的那一部分
            int m2 = m - m1;                    // m2为D的位数，C属于高位的那一部分
            std::string A = s.substr(0, n2);    // 获取s的高位部分A
            std::string B = s.substr(n2);       // 获取s的低位部分B
            std::string C = t.substr(0, m2);    // 获取t的高位部分C
            std::string D = t.substr(m2);       // 获取t的低位部分D
            multiply(A, C, pos + n1 + m1);      // AC,在result[pos+n1+m1]的位置存储AC，也是说偏移pos+n1+m1位，pos初始化为0
            multiply(B, C, pos + m1);           // BC,偏移pos+m1位
            multiply(A, D, pos + n1);           // AD,偏移pos+1位
            multiply(B, D, pos);                // BD,偏移pos位
        }
    };
    multiply(X, Y, 0);

    int len = (int) X.size() + (int) Y.size();
    for (int i = 0; i <= len; i++) {
        int now = result[i] % 10;
        int bit1 = result[i] / 10 % 10;
        int bit2 = result[i] / 100;
        result[i] = now;
        result[i + 1] += bit1;
        result[i + 2] += bit2;
    }
    while (result.back() == 0) {
        result.pop_back();
    }

    return result;
}

方法三：FFT

时间复杂度：$O(nlogn)$

通过分治的思想，最终演变成FFT的雏形，FFT的思想也是分治，但是它的理论要更为深奥。 为了避免精度问题，可以改用快速数论变换FNTT。 具体可以看这篇文章的推导

方法四：中国剩余定理

把每个数分解到一些互素的模上，然后每个同余方程对应乘起来就行。

方法五：网络流

补

方法六: Furer’s algorithm

在渐进意义上FNTT还快的算法。不过好像不太实用，本文就不作介绍了。大家可以参考维基百科Fürer’s algorithm

本文作者：jujimeizuo
本文地址： https://blog.jujimeizuo.cn/2022/12/06/bigintegermultiply/
本博客所有文章除特别声明外，均采用 CC BY-SA 3.0 协议。转载请注明出处！