曼哈顿距离
定义两个点 $A(x_1, y_1), B(x_2, y_2)$,则 $A, B$ 之间的曼哈顿距离为:
$$
d(A, B) = |x_1 - x_2| + |y_1 - y_2|
$$
性质
- 对称性:$d(A,B)=d(B,A)$
- 三角不等式:$d(A,C) \le d(A,B)+d(B,C)$
距离原点的曼哈顿距离为 1 组成的点:
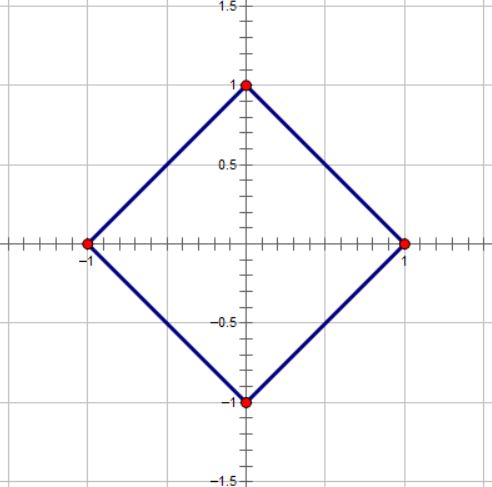
切比雪夫距离
定义两个点 $A(x_1, y_1), B(x_2, y_2)$,则 $A, B$ 之间的切比雪夫距离为:
$$
d(A, B) = \max ( |x_1 - x_2|, |y_1 - y_2| )
$$
距离原点的切比雪夫距离为 1 组成的点:
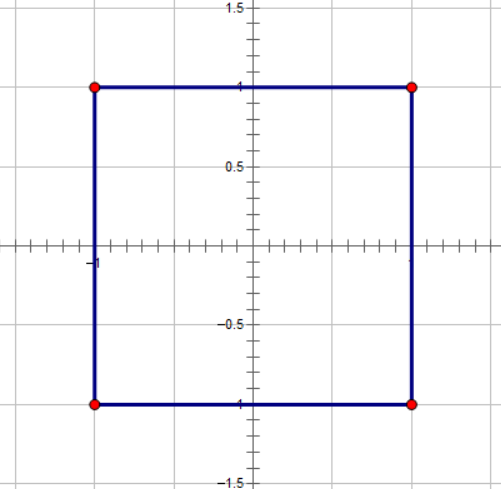
转换
曼哈顿转切比雪夫
将代表曼哈顿距离的正方形绕原点逆时针旋转 $\frac{\pi}{4}$,发现两个正方形是相似的,只需要把代表曼哈顿距离的正方形扩大 $\sqrt{2}$ 倍。
发现原来在代表曼哈顿距离的正方形的四条边上的点 $A(x,y)$ 的坐标由旋转之后变为了
$$(x * \cos{\frac{\pi}{4}}-y * \sin{\frac{\pi}{4}}, y * \cos{\frac{\pi}{4}} + x * \sin{\frac{\pi}{4}})$$
然后扩大后变为
$$A^\prime(\sqrt{2}(x * \cos{\frac{\pi}{4}}-y * \sin{\frac{\pi}{4}}), \sqrt{2}(y * \cos{\frac{\pi}{4}} + x * \sin{\frac{\pi}{4}})) \to A^\prime (x-y, x+y)$$
这里的旋转事实上可以理解为坐标轴的旋转。
切比雪夫转曼哈顿
通过图形旋转,原来的点 $A(x,y) \to A^\prime(\frac{x+y}{2}, \frac{x-y}{2})$。(由上述逆变换证明)
恒等式
$$
|x_1 - x_2| + |y_1 - y_2| = \max(|x_1^\prime - x_2^\prime|, |y_1^\prime - y_2^\prime|)
$$
其中等式左侧为 $(x_1,y_1)$ 和 $(x_2, y_2)$ 的曼哈顿距离,等式右侧 $(x^\prime - y^\prime)=(x+y,y-x)$,计算的是 $(x_1^\prime - y_1^\prime)$ 和 $(x_2^\prime - y_2^\prime)$ 两点的曼哈顿距离投影到 $x^\prime$ 轴和 $y^\prime$ 轴的线段长度的最大值,即切比雪夫距离。
Reference
本文作者:jujimeizuo
本文地址: https://blog.jujimeizuo.cn/2024/04/01/Manhattan-and-Chebyshev-switch/
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0 协议。转载请注明出处!