6.1 DCT变换
- DCT变换避免了复述运算。由于图像矩阵是实数矩阵,那么它的DCT也是实数。
- DCT是正交变换,其变换矩阵是正交阵,变换核是可分离的。
- DCT与IDCT具有相同的变换核,因此具有相同的变换矩阵,即正变换与逆变换公用同一个算法模块。
- DCT具有更强的信息集中能力,能将最多的信息放到最少的系数上。
6.1.1 一维DCT变换
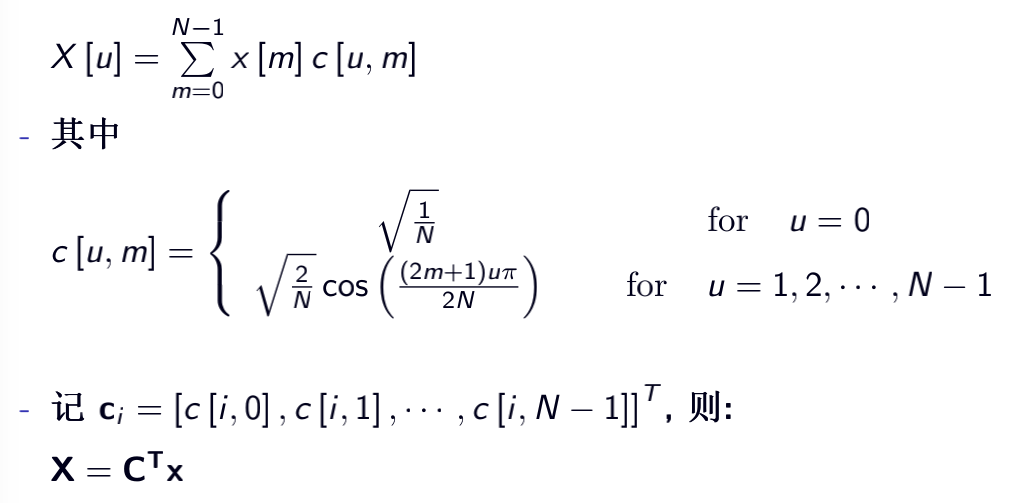

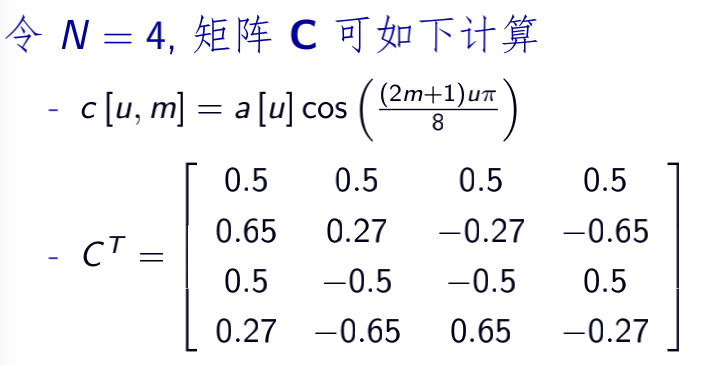

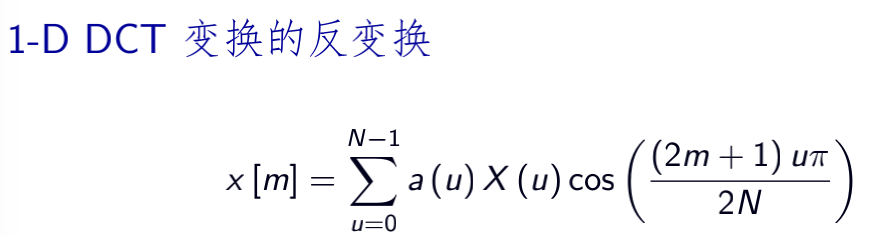

6.1.2 二维DCT变换


6.2 图像编码基础
6.2.1 图像压缩的基本概念
定义: 减少表示图像的数据量
- 在图像传输的时候,可传输较少的数据量,但不减少图像所表达的信息量
- 在图像存储时,可减少所需的存储空间,同时较少存储所需的时间
图像信息可以压缩的根据
- 图像信号存在大量的冗余
- 可以利用人的视觉特性
图像信息的冗余度表现在结构和统计两个方面
图像信息结构上冗余度表现为:图像具有很强的空间(帧内)相关性和时间(帧间)相关性。
编码冗余、像素间冗余、心理-视觉冗余、帧间冗余。
获取图像压缩质量的好坏是通过计算其压缩比得到的,公式为:
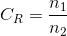

图像熵数学公式为:
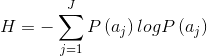

6.2.2 图像编码模型
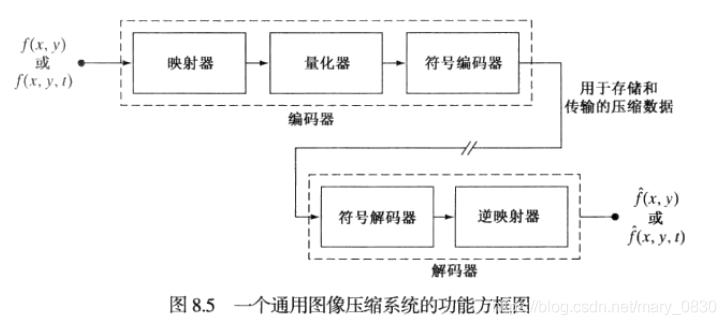

6.3 霍夫曼码
6.3.1 概念
哈夫曼编码是可变字长编码(VLC)的一种。该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。通俗来说就是,信源符号出现频率越高,使用的码字就越少。
6.3.2 编码过程
- 对符号的概率进行排序,建立信源递减序列;
- 对每个约简的信源进行编码,从最小的信源开始,已知到原始信源。
6.3.3 霍夫曼编码
霍夫曼码的产生不是压缩过程。为了实现成为霍夫曼码的压缩,对于产生码字的符号,不管它们的灰度级、行程长度,还是其他灰度映射操作的输出,都必须在生成码字一致的情况下被变换或映射。
霍夫曼树─即最优二叉树,带权路径长度最小的二叉树,经常应用于数据压缩。 在计算机信息处理中,“霍夫曼编码”是一种一致性编码法(又称“熵编码法”),用于数据的无损耗压缩。
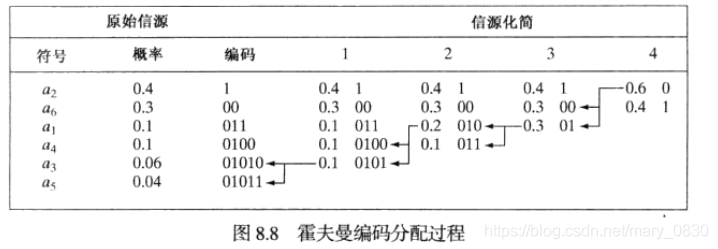
霍夫曼编码的原理: 霍夫曼方法的第一步是通过对所考虑符号的概率进行排序,并将具有最小概率的符号合并为一个符号来替代下次信源化简过程中的符号,从而创建一个简化信源系列。如下图所示那样,载最左边一组虚构的信源符号集合及它们的概率根据概率值的减少从上到下排列,为了形成第一次信源简化,底部的两个概率0.06和0.04进行合并,形成一个概率值为0.1的“复合符号”,这个复合符号及其对应的概率被置于第一个信源简化的列中,以便简化后的信源概率仍然按照其值从大到小进行排列,这个过程一直重复持续到信源只有两个符号的简化信源为止。

6.3.4 霍夫曼译码
经过霍夫曼编码再译码之后,才获得有用的图像,译码器必须计算用来编码x的霍夫曼码,再反映射已编码的数据来重建x,这是一种逆过程,但是缺少了反量化的步骤(这是不可逆转的一步)。
本文作者:jujimeizuo
本文地址: https://blog.jujimeizuo.cn/2021/06/20/shuzituxiang6/
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0 协议。转载请注明出处!