8.1 图像纹理的主要特征及描述与提取方法
8.1.1 图像纹理的主要特征
- 粗糙度
- 方向性
- 规则性
8.1.2 图像纹理特征及描述与提取方法
- 统计分析法
- 结构分析法
- 模型分析法
- 频谱分析法
8.2 基于灰度共生矩阵的纹理特征提取方法
8.2.1 概念及定义
灰度共生矩阵定义为像素对的联合概率分布，是一个对称矩阵，它不仅反映图像灰度在相邻的方向、相邻间隔、变化幅度的综合信息，但也反映了相同的灰度级像素之间的位置分布特征，是计算纹理特征的基础。
在图像中任意取一点(x,y)及偏离它的一点(x+a,y+b)(其中，a、b为整数，人为定义)构成点对。设该点对的灰度值为(f1,f2)，再令点(x,y)在整幅图像上移动，则会得到不同的(f1,f2)值。
设图像的最大灰度级为L，则f2与f2的组合共有L*L种。对于整幅图像，统计出每一种(f1,f2)值出现的次数，然后排列成一个方阵，再用(f1,f2)出现的总次数将他们归一化为出现的概率P(f1,f2)，由此产生的矩阵为灰度共生矩阵。θ方向上的间隔为d的灰度共生矩阵实际上是θ方向间隔为d的灰度变化量的联合概率分布。
8.2.2 共生矩阵的计算
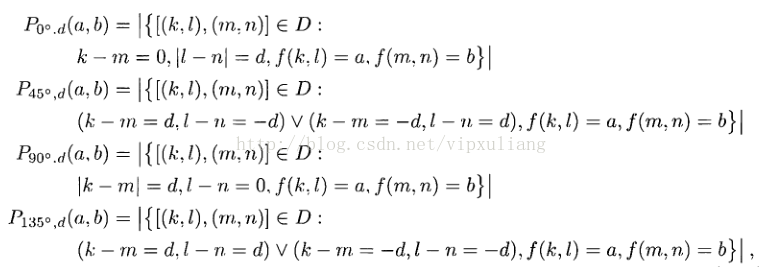公式(1)中d表示像素间隔，(k,l), (m,n)分别为原像素和偏移后的像素坐标，其中k,m为纵坐标，D为图像范围。 举例说明，假设原图像如图1.a所示 
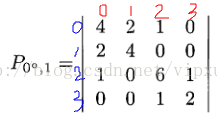
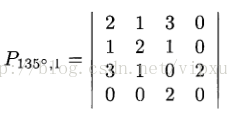对1.b中蓝色字表示原像素灰度值，红字为偏移后像素灰度值。则对矩阵元素P0°,1 (0,0)表示1.a中在0°方向上（包括正和负方向）相距为1的(0,0)点对有两对，考虑正负方向的加倍效果，P0°,1 (0,0)=4。同样由于公式(1)对距离d定义的双向性，使得灰度共生矩阵为对称矩阵。
为了减小计算量，可将d定义为沿θ正方向。则(1)式变为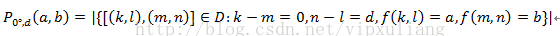 
由1.a得到的新的灰度共生矩阵为 
本文作者：jujimeizuo
本文地址： https://blog.jujimeizuo.cn/2021/06/20/shuzituxiang8/
本博客所有文章除特别声明外，均采用 CC BY-SA 3.0 协议。转载请注明出处！