问题描述
表达式求值要解决的问题一般是输入一个字符串表示的表达式,要求输出它的值。当然也有变种比如表达式中是否包含括号,指数运算,含多少变量,判断多个表达式是否等价,等等。
表达式一般需要先进行语法分析(grammer parsing)再求值,也可以边分析边求值,语法分析的作用是检查输入的字符串是否是一个合法的表达式,一般使用语法分析器(parser)解决。
表达式包含两类字符:运算数和运算符。对于长度为n的表达式,借助合适的分析方法,可以在 $O(n)$的时间复杂度内完成分析与求值。
表达式树与逆波兰表达式
一种递归分析表达式的方法是,将表达式当成普通的语法规则进行分析,分析后拆分成如图所示的
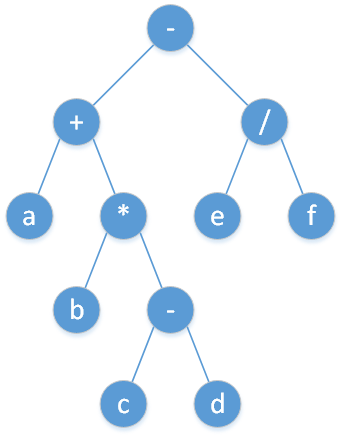
表达式树,然后在树结构上自底向上进行运算。
表达式树上进行 树的遍历 可以得到不同类型的表达式。算术表达式分为三种,分别是前缀表达式、中缀表达式、后缀表达式。中缀表达式是日常生活中最常用的表达式;后缀表达式是计算机容易理解的表达式。
前序遍历对应前缀表达式(波兰式) 中序遍历对应中缀表达式 后序遍历对应后缀表达式(逆波兰式) 逆波兰表达式(后缀表达式)是书写数学表达式的一种形式,其中运算符位于其操作数之后。例如,以下表达式:
$$a+b_c_d+(e-f)_(g_h+i)$$
可以用逆波兰表达式书写:
$$abc_d_+ef-gh_i+_+$$
因此,逆波兰表达式与表达式树一一对应。逆波兰表达式不需要括号表示,它的运算顺序是唯一确定的。
逆波兰表达式的方便之处在于很容易在线性时间内计算。举个例子:在逆波兰表达式32*1- 中,首先计算 3*2=6(使用最后一个运算符,即栈顶运算符),然后计算6-1=5 。可以看到:对于一个逆波兰表达式,只需要 维护一个数字栈,每次遇到一个运算符,就取出两个栈顶元素,将运算结果重新压入栈中。最后,栈中唯一一个元素就是该逆波兰表达式的运算结果。该算法拥有O(n) 的时间复杂度。
只含左结合的二元运算符的含括号表达式
考虑简化的问题。假设所有运算符都是二元的:所有运算符都有两个参数。并且所有运算符都是左结合的:如果运算符的优先级相等,则从左到右执行。允许使用括号。
对于这种类型的中缀表达式的计算,可以将其转化为后缀表达式再进行计算。定义两个 栈 来分别存储运算符和运算数,每当遇到一个数直接放进运算数栈。每个运算符块对应于一对括号,运算符栈只对于运算符块的内部单调。每当遇到一个操作符时,要查找运算符栈中最顶部运算符块中的元素,在运算符块的内部保持运算符按照优先级降序进行适当的弹出操作,弹出的同时求出对应的子表达式的值。
以下部分用「输出」表示输出到后缀表达式,即将该数字放在运算数栈上,或者弹出运算符和两个操作数,运算后再将结果压回运算数栈上。从左到右扫描该中缀表达式:
- 如果遇到数字,直接输出该数字。
- 如果遇到左括号,那么将其放在运算符栈上。
- 如果遇到右括号,不断输出栈顶元素,直至遇到左括号,左括号出栈。换句话说,执行一对括号内的所有运算符。
- 如果遇到其他运算符,不断输出所有运算优先级大于等于当前运算符的运算符。最后,新的运算符入运算符栈。
- 在处理完整个字符串之后,一些运算符可能仍然在堆栈中,因此把栈中剩下的符号依次输出,表达式转换结束。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| std::unordered_map<char, int> level = {
{'+', 0}, {'-', 0}, {'*', 1}, {'/', 1}, {'(', -1}, {')', -1}
};
std::string infixToSuffix(const std::string& expression) {
std::string suffix_expression;
std::vector<char> oper;
for (int i = 0; i < (int) expression.size(); i += 1) {
if (expression[i] == ' ') {
continue;
} else if (isdigit(expression[i])) {
while (i < (int) expression.size() && isdigit(expression[i])) {
suffix_expression.push_back(expression[i]);
i += 1;
}
suffix_expression.push_back(' ');
i -= 1;
} else if (expression[i] == '(') {
oper.push_back('(');
} else if (expression[i] == ')') {
while (!oper.empty() && oper.back() != '(') {
suffix_expression.push_back(oper.back());
suffix_expression.push_back(' ');
oper.pop_back();
}
oper.pop_back();
} else {
while (!oper.empty() && level[oper.back()] >= level[expression[i]]) {
suffix_expression.push_back(oper.back());
suffix_expression.push_back(' ');
oper.pop_back();
}
oper.push_back(expression[i]);
}
}
while (!oper.empty()) {
suffix_expression.push_back(oper.back());
suffix_expression.push_back(' ');
oper.pop_back();
}
return suffix_expression;
}
long long calc(const std::string expression) {
auto suffix_expression = infixToSuffix(expression);
std::vector<long long> nums;
std::stringstream ss;
ss << suffix_expression;
std::string s;
while (ss >> s) {
if (isdigit(s[0])) {
nums.push_back(stoi(s));
} else {
long long b = nums.back();
nums.pop_back();
long long a = nums.back();
nums.pop_back();
if (s[0] == '+') nums.push_back(a + b);
else if (s[0] == '-') nums.push_back(a - b);
else if (s[0] == '*') nums.push_back(a * b);
else if (s[0] == '/') nums.push_back(a / b);
}
}
return nums.back();
}
|
本文作者:jujimeizuo
本文地址: https://blog.jujimeizuo.cn/2022/12/06/expression/
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0 协议。转载请注明出处!
